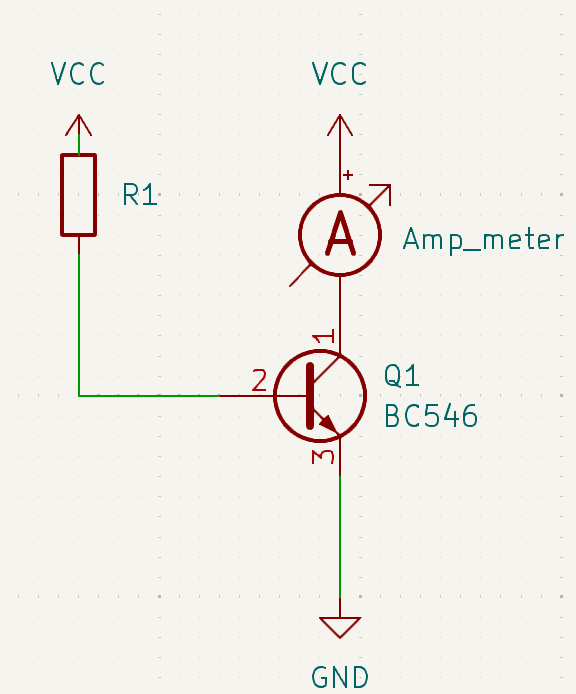
Theoretical current source

In these formulas, \(I_B\) represents the base current of the transistor, \(I_o\) is the current sourced by the circuit, and \(\beta\) denotes the low-frequency current gain (amplification factor). $$ I_B = {V_{cc}-U_{BE} \over R_1}$$ $$ I_o = \beta * I_B$$ $$ I_o = {\beta * (V_{cc}-U_{BE}) \over R_1}$$ The issue with this type of source lies in the direct dependence of \(I_o\) on the supply voltage (\(V_{cc}\)), the base-emitter voltage (\(U_{BE}\)), and the amplification factor (\(\beta\)). Both \(U_{BE}\) and \(\beta\) are temperature-dependent: \(U_{BE}\) decreases approximately by 2 mV per degree Celsius, while \(\beta\) increases with rising temperature. These variations cause an increase in \(I_o\), potentially leading to thermal runaway. For this reason, such a source is not recommended.

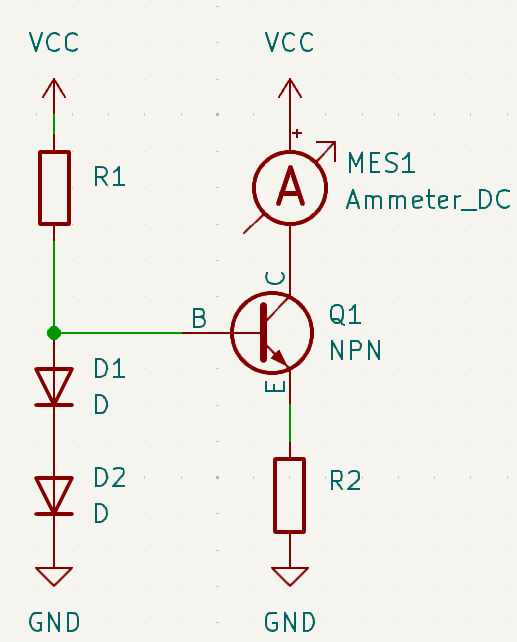
Simple current source

The simplest current source that can be constructed is a single-transistor source with a base and emitter resistor. The current \(I_o\) can be calculated using the following formulas: $$ V_{cc}=U_{R1}+U_{BE}+U_{R2}$$ $$ U_{R1}=I_B*R_1 $$ $$ U_{R2}=I_{R2}*R_2 $$ $$ I_{R2} = I_o+I_B $$ $$ I_o = \beta * I_B$$ $$ I_o = {\beta * (V_{cc}-U_{BE}) \over R_1+R_2+R_2*\beta}$$ Again the issue with this type of source lies in the direct dependence of \(I_o\) on the supply voltage (\(V_{cc}\)), the base-emitter voltage (\(U_{BE}\)), and the amplification factor (\(\beta\)). Both \(U_{BE}\) and \(\beta\) are temperature-dependent: \(U_{BE}\) decreases approximately by 2 mV per degree Celsius, while \(\beta\) increases with rising temperature. These variations cause an increase in \(I_o\), which gets reduced by the Emitter resistor, as an increase in \(I_o\) leads to a higher voltage drop across the resistor. This increased loss does decrease the base current. If a emitter resistor is choosen its benificial to use one with a positive thermal resistance change. This is mendaory to cancle the thermal runaway and does reduce the current at high operation temperatures. Nevertheless such a source is not recommended.

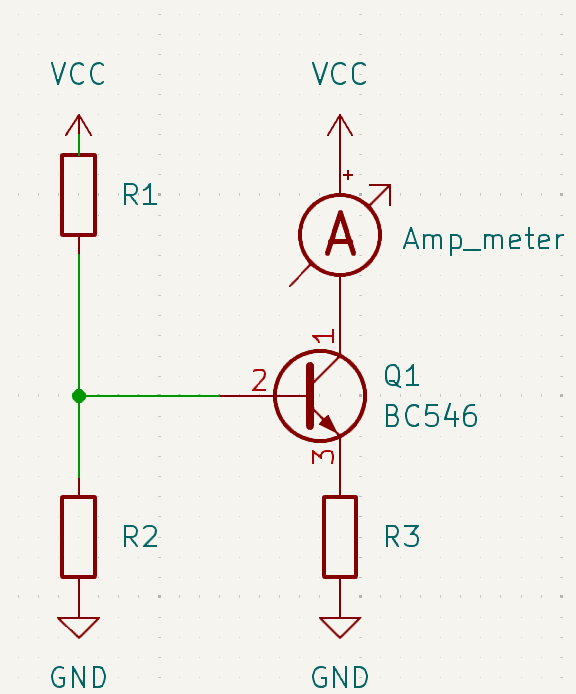
Voltage divider current source

To further minimize the transistor's dependence on the supply voltage, a voltage divider can be added as a reference. The sourced current Io can be calculated using the following formulas: $$ V_{cc}=U_{R1}+U_{BE}+U_{R3}$$ $$ U_{R1}=(I_B+I_{R2})*R_1 $$ $$ U_{R2}=U_{R3}+U_{BE} $$ $$ U_{R3}=I_{R3}*R_3 $$ $$ I_{R3}=I_o+I_B $$ $$ I_{R2}={U_{R2} \over R_{2}}$$ $$ I_o = \beta * I_B$$ $$ I_o = {\beta * (V_{cc}*R_1-R_1*U_{BE}-R_2*U_{BE}) \over R_1*R_2+R_1*R_3+R_1*R_3*\beta+R_2*R_3+R_2*R_3*\beta}$$ In these formulas, \(I_B\) represents the base current of the transistor, while \(I_o\) is the current sourced by the circuit. \(\beta\) denotes the low-frequency amplification factor. By incorporating a voltage divider as a reference, it is possible to further reduce the dependence on the supply voltage;

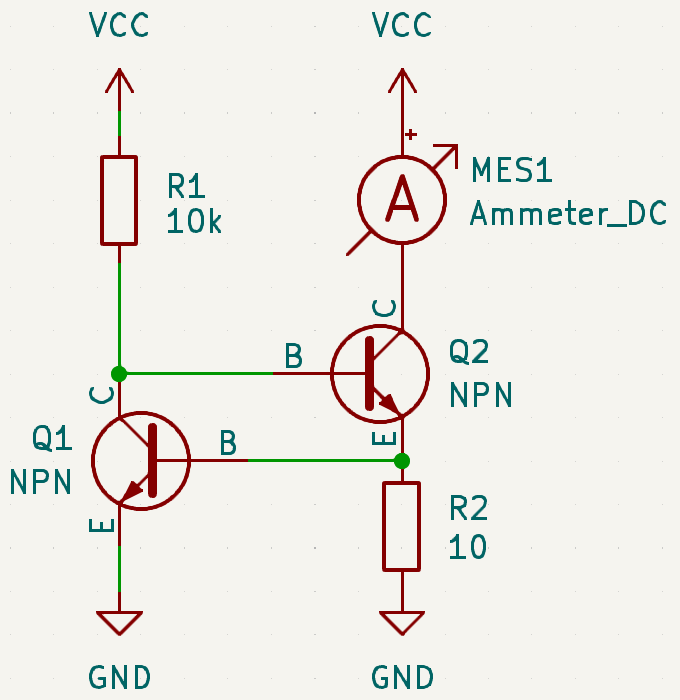
Dual Tranistor current source

The use of a dual-transistor source offers two key benefits. First, it provides a source with a positive temperature coefficient, which prevents thermal runaway. Second, it requires only a very low dropout voltage above \(R_{2}\). The source current can be calculated using the following formulas: $$ V_{cc}=U_{R1}+U_{BE1}+U_{R2}$$ $$ 0 = -U_{BE2}+U_{R2} $$ $$ U_{R1}=I_{R1}*R_1 $$ $$ U_{R2}=I_{R2}*R_2 $$ $$ 0=I_{R1}-I_{B2}-I_{C1} $$ $$ I_o=I_o+I_{BE2}-I_{BE1}-I_{R2}$$ $$ I_o = \beta_2 * I_{B2}$$ $$ I_{C1} = \beta_1 * I_{B1}$$ $$ I_o = {\beta_2 * (V_{cc}-U_{BE1}-U_{BE2}+{R1*\beta_1*U_{BE2} \over R_2}) \over R_1+R_1*\beta_1+R_1*\beta_1*\beta_2}$$ Incorporating the two transistors as switching devices worsens the temperature behavior, as the current decreases rapidly with rising temperature. While this results in a stable source, it is not very accurate.

To significantly enhance the thermal stability of the sources, it is essential to address the issue at its core: the thermal dependence of the base-emitter \(BE\) diode and, consequently, the base current (\(I_b\)). This dependence can be mitigated by continuously adjusting the supplied base-emitter voltage (\(U_{BE}\)) to match the transistor's own base-emitter voltage characteristics. This adjustment can be achieved by creating a thermal drift in the supply voltage that mirrors the thermal drift of the transistor. There are various methods to accomplish this, and two straightforward examples will be discussed here.

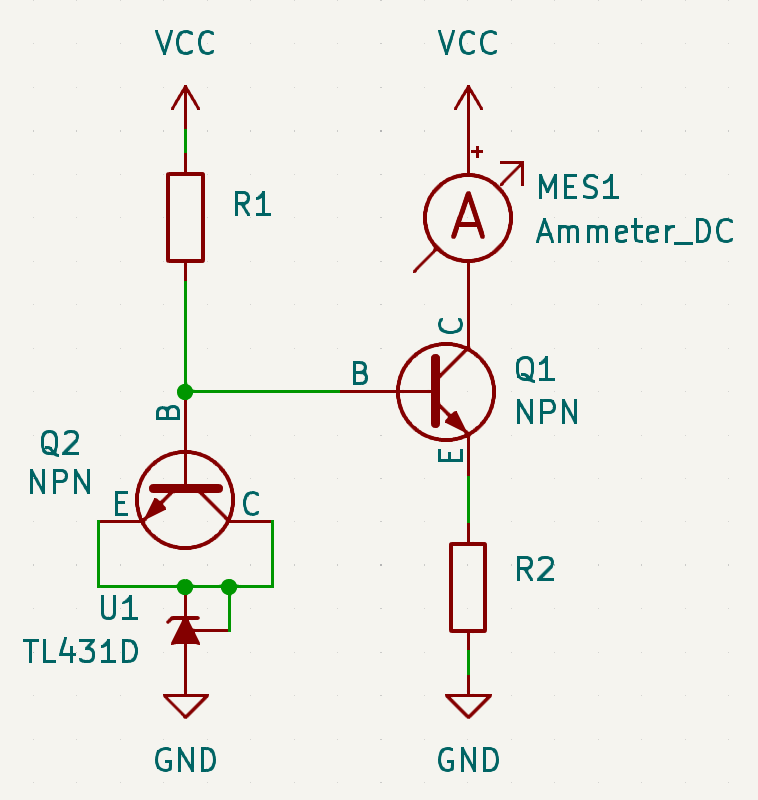
Diode compenstated mcurrent source

To create a temperature-compensated source, it is essential to generate a base voltage that matches the temperature characteristics of the transistor. This can be approximated by using a diode. The current for this source can be calculated using the following formulas: $$ V_{cc}=U_{R1}+U_{D1}+U_{D2}$$ $$ V_{cc}=U_{R1}+U_{BE}+U_{R2} $$ $$ U_{R2}=I_{R2}*R_2 $$ $$ I_{R2} = I_B+I_o$$ $$ I_o = \beta * I_{B}$$ $$ I_o = {\beta*(U_{D1}+U_{D2}-U_{BE}) \over R_2+R_2*\beta}$$ If standard silicon diodes are used, two are required to achieve a base voltage higher than that of the transistor. Unfortunately, this eliminates thermal compensation because the thermal variations of the two diodes combine and overcompensate for the transistor.
To address this, a single high-dropout diode, such as an LED, is recommended. Alternatively, a Zener diode can also be used.
For a higher degree of thermal compensation, it is beneficial to use a transistor of the same type as the one being compensated, configured to function as a diode. The offset level can then be established using a precision reference.