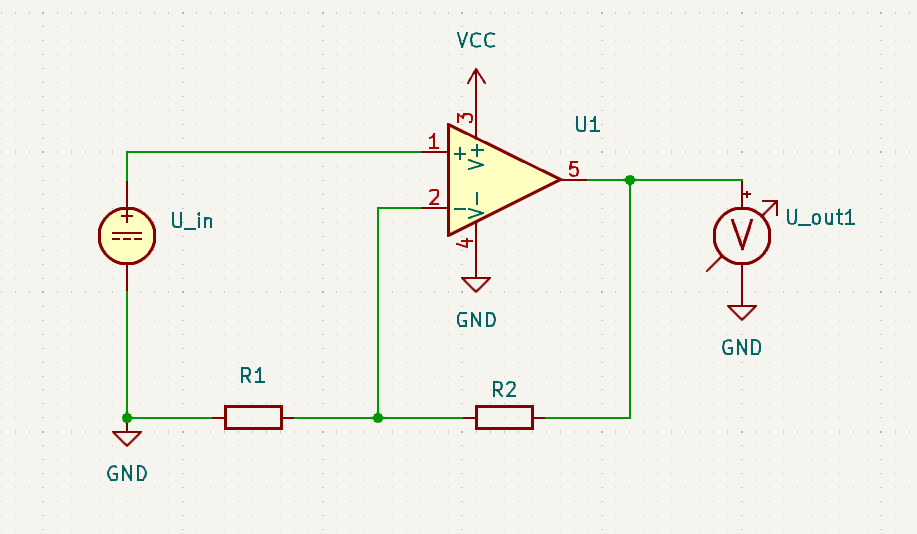
To analyze this circuit, the operational amplifier is assumed to be ideal, meaning:
In these formulas, \(I_{ges}\) represents the current flowing through \(R_1\) and \(R_2\).
\(U_D\) is the voltage difference between the non-inverting (+) and inverting (-) terminals.
\(U_{in}\) and \(U_{out}\) are the input and the output voltages, respectively.
$$ I_{ges} = {U_{out} \over {R_1+R_2}}$$ $$ U_{D} = 0 $$ $$ I_{R1} = {U_{in} \over R_1} $$ $$ I_{ges} = I_{R1} = I_{R2} $$ $$ {U_{out} \over {R_1+R_2}} = {U_{in} \over R_1} $$ $$ v = {U_{out} \over U_{in}} = {{R_1 +R_2} \over R_2} = 1+{R_1 \over R_2} $$ These formulas demonstrate that the amplification factor is always greater than 1. Additionally, they indicate that the circuit's input resistance is effectively infinite.
- The differential input voltage \(U_D\) is zero, implying no input offset voltage.
- The output offset voltage is zero.
- The input current is negligible (zero). / The input resistance is infinite.
- The output resistance is zero.
- The open-loop gain is infinite.
In these formulas, \(I_{ges}\) represents the current flowing through \(R_1\) and \(R_2\).
\(U_D\) is the voltage difference between the non-inverting (+) and inverting (-) terminals.
\(U_{in}\) and \(U_{out}\) are the input and the output voltages, respectively.
$$ I_{ges} = {U_{out} \over {R_1+R_2}}$$ $$ U_{D} = 0 $$ $$ I_{R1} = {U_{in} \over R_1} $$ $$ I_{ges} = I_{R1} = I_{R2} $$ $$ {U_{out} \over {R_1+R_2}} = {U_{in} \over R_1} $$ $$ v = {U_{out} \over U_{in}} = {{R_1 +R_2} \over R_2} = 1+{R_1 \over R_2} $$ These formulas demonstrate that the amplification factor is always greater than 1. Additionally, they indicate that the circuit's input resistance is effectively infinite.